DFG (Deutsche Forschungsgemeinschaft) project BA 2823/8-1 within the SPP (German Priority Program) 1648 "SPPEXA" (Software for Exascale Computing)
Cooperation with:
A. Klawonn (Universität zu Köln),
O. Rheinbach (Technische Universität Bergakademie Freiberg),
J. Schröder (Universität Duisburg-Essen),
G. Wellein (Friedrich-Alexander-Universität Erlangen-Nürnberg)
Abstract:
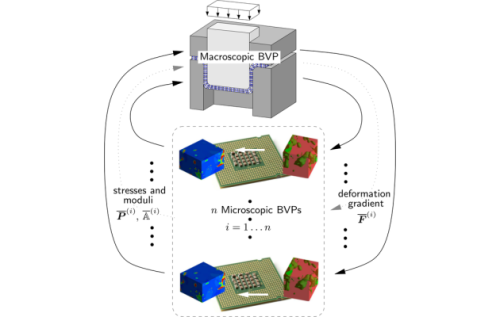
The project EXASTEEL in the SPP 1648 deals with the computational simulation of advanced high strength steels, incorporating phase transformation phenomena at the microscale using the FE² direct multiscale approach. Thereby in each macroscopic integration point an additional (microscopic) boundary value problem is solved and suitable volume averages of the microscopic responses replace the macroscopic constitutive set of equations compared to classical FEM computations. In a serial set-up this procedure results in high numerical costs especially in the three dimensional case. New, highly efficient, parallel solver algorithms will enable the FE² approach to perform simulations of three dimensional multiscale material science problems. Due to the main objectives of SPPEXA, here the development for the exascale computing on future supercomputers is one of the main aspects.

DFG (Deutsche Forschungsgemeinschaft) project no SCHR 570-8/2 (research group 797 "microplast")
Cooperation with:
J. Schröder (Universität Duisburg-Essen),
D. Raabe (Max-Planck Institut für Eisenforschung GmbH)
Abstract:
Micro-heterogeneous high-tech steels enable ambitious engineering constructions. For the design of such random multi-phase microstructures numerical simulation procedures are important for the reliable prediction of the overall response of macroscopic boundary value problems. Direct homogenization schemes, which are designed for such kind of problems, can only be efficient if the complex random microstructure is approximated by significantly less complex representative volume elements (RVEs) capturing the basic morphological attributes of the microscale. This is the main task in the project, where several statistical measures (spectral-density, lineal-path function, Minkowski valuations, etc.) are applied for the construction of statistically similar RVEs (SSRVEs). A main challenge in this period is the design of three-dimensional SSRVEs based on the Electron-Backscatter Diffraction (EBSD) combined with Focused-Ion-Beam (FIB) measurements. The performance of the direct homogenization approach using the constructed SSRVEs is analyzed for representative macroscopic deep-drawing processes.
References:
Cooperation with:
N. Stranghöner (Universität Duisburg-Essen)
Abstract:
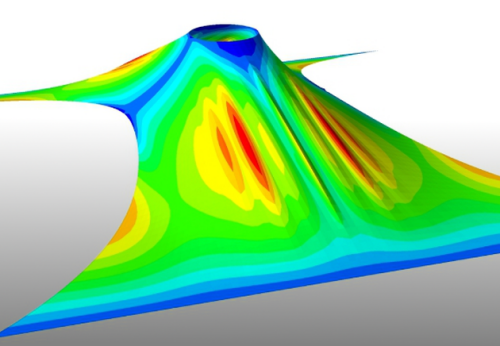
The simulation of textile membranes in civil engineering practice is currently based on strong simplifications of the material description. Although the materials show a highly nonlinear stress-strain response in biaxial tension tests, linear elastic models are applied. Furthermore, membrane formulations or approaches based on cord networks are typically used for the numerical calculation of structures which are not capable of reliably predicting e.g. wrinkle formation. In order to improve the current state of the art, in this project new models are developed which describe the material behavior more accurately by taking into account a fully nonlinear continuum mechanical framework.
The models are however constructed such that a practical application may still be enabled.
In addition to that, shell finite element formulations are applied to account for wrinkling.
References:
Cooperation with:
Daniel Peterseim (Universität Augsburg, Numerische Mathematik)
M. A. Peter (Universität Augsburg, Angewandte Analysis)
M. Ortiz (California Institute of Technology CALTECH, Pasadena, USA)
Abstract:
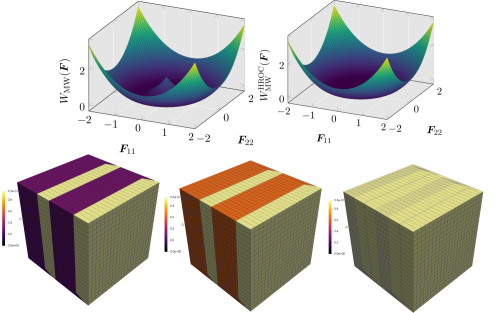
Our project investigates the formidable challenge of predicting progressive material degradation, particularly in soft biological tissues and engineered systems subjected to mechanical stress. With a specific focus on damage mechanisms within arterial walls—influenced by atherosclerotic plaque development and interventional procedures like angioplasty—we develop computational frameworks designed to capture the complex interplay of stress-softening, hysteresis, and strain-softening phenomena. A fundamental hurdle is the inherent ill-posedness of classical damage models; this arises from the non-convexity of the underlying energy landscapes, leading to undesirable mesh-dependent localization effects.
Traditional strategies for addressing these instabilities rely on regularization techniques, including spatial methods like gradient-enhanced formulations and phase-field models, alongside temporal approaches that incorporate rate-dependent viscosity. However, our project centers on an alternative approach known as relaxation. Here, we replace non-convex energy densities with their corresponding semiconvex envelopes, effectively recovering a well-posed problem. This method elegantly avoids the introduction of artificial length scales or rate dependencies, and instead characterizes damage through homogenized microstructural patterns inherently encoded within oscillating gradients. While analytical relaxation can furnish exact solutions for simplified cases, such as hyperelastic materials, practical applications involving finite-strain damage in complex materials like arteries necessitate robust numerical approximations.
To this end, our contributions encompass hierarchical rank-one convexification techniques and adaptive convexification strategies specifically tailored for microsphere-based models. These techniques are designed to bridge the scales between microscopic cavitation events and macroscopic softening behaviors. Recent advancements leverage optimization-based frameworks, iteratively approximating semiconvex envelopes directly within finite element computations. While these methods hold substantial promise for clinical applications—for example, optimizing stent placement to minimize iatrogenic arterial injury—significant challenges remain in simultaneously achieving computational efficiency and maintaining rigorous physical fidelity, particularly when confronted with inelastic and large-strain scenarios. Ongoing collaborative efforts are directed toward continually refining discretization schemes and rigorously validating our models against experimental datasets, with the ultimate goal of advancing predictive capabilities across both biomedical and industrial applications.
References:
Abstract:
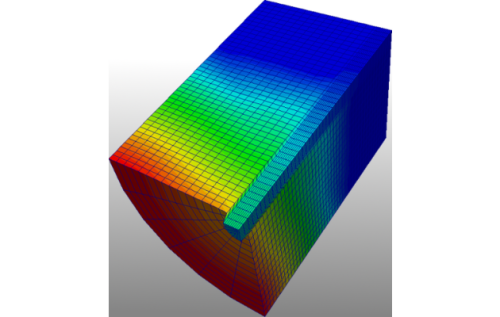
Pre-damaged structures made of fiber reinforced composite materials preserve their structural integrity under dynamic loads due to crack-bridging effects of the reinforcement fiber. Under dynamic loads, which leads to relative displacements of the crack edges, the crack-bridging fibers are stretched and further pulled out of the surrounding matrix. Main scope of the research project is the modeling of the successive strip away of the fibers from the matrix, which is mainly influenced by the (tensile) wave propagation in the fiber and reverse influences the wave propagation of the surrounding matrix. The investigations deal with the pull of modern fiber reinforcements out of brittle matrices like concrete
References:
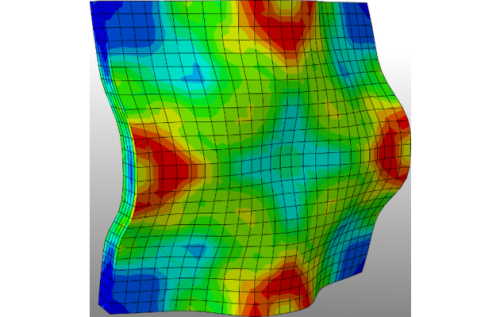
Abstract:
Impact loads lead to high stresses in fiber reinforced concrete structures. In order to protect people, animals and goods, the constructed structures need a high impact resistance. This research project focusses on the multiscale modeling of processes in the material due to the impact loading. Special attention is paid to the phenomena of wave propagation, damping and anisotropic damage including composite failure. Another aim of the project is the provision of appropriate representative volume elements at the lower scale.
References:
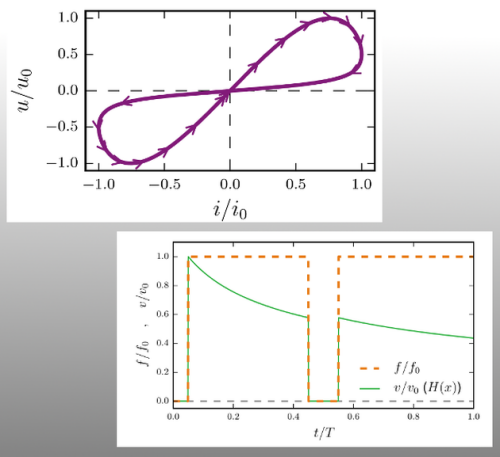
Cooperation with:
A. Franze (Institute of Mechanics and Shell Structures, Technical University Dresden)
Abstract:
This project treats deals with the dynamic behavior of materials with memristive properties. Here, the notion of memristance is inherited from electrical engineering. It describes the behavior of so called memristors, which are non-linear resistors with a memory function. Transferred to mechanics, memristive behaviour describes a non-linear, history dependent material with damping properties. The objective of these investigations are efficient methods that can compute structures with memristive material properties.
References:
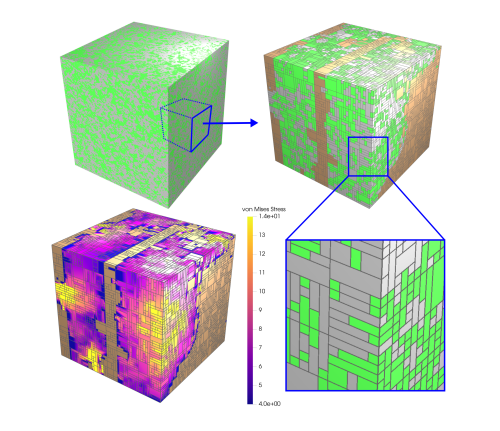
Project C6 within the SFB (Sonderforschungsbereich) 837 „Interaction Modeling in Mechanized Tunneling“
Coorporation with:
K. Hackl (Ruhr-Universität Bochum)
Abstract:
Wear of the mining tools of the mechanized tunneling machines reduces the efficiency of the tunneling process. In order to gain a deeper understanding of the wear process, to predict the life time of the mining tools and from that, to optimize them regarding wear, this project deals with modeling and simulation of the mining tools. Therefore, the two involved wear mechanisms, surface disruption and abrasion, are investigated. For the modeling of the surface disruption on the microscale, the Finite Cell Method (FCM) is combined with the eigenerosion algorithm to simulate ductile crack propagation. This method is applied on Statistically Similar Representative Volume Elements (SSRVE) that are generated computationally based on XRCT scans of the metallic microstructure. The overall material behavior is obtained by homogenization with the mean field method. For investigating the abrasive wear on the macroscale, a damage-plasticity material model is developed. Additionally, the influence of the soil on the wear of the mining tools is obtained by simulating simple scratch tests with the Discrete Element Method (DEM).
References: